P vs. NP

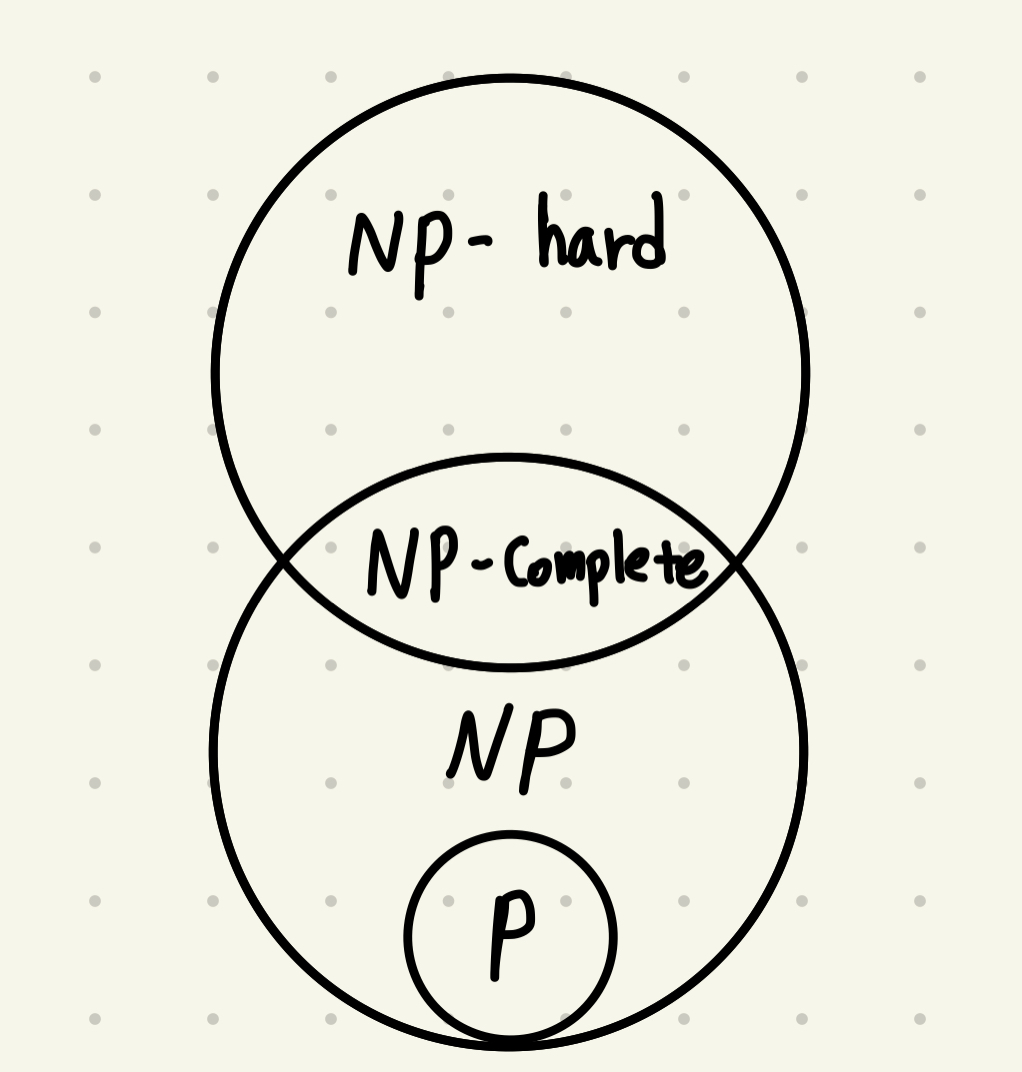
The P-NP problem is an unsolved problem in theoretical computer science regarding whether complexity classes P and NP are equivalent. In brief, it asks whether problems that can be verified quickly can also be solved quickly.

P(Polynomial):

• Set of problems that can be solved in polynomial time(time that can be expressed by a polynomial, with variables from the algorithm's input) on a deterministic Turing machine

ex) Bubble sort has a polynomial of n(n-1)/2. It is a quadratic polynomial in terms of n.

NP(Non-deterministic Polynomial):

• Set of Problems that can be solved in polynomial time on a non-deterministic Turing machine
• Set of problems that can be verified in polynomial time.

ex) Subset problem requires only add operation if relying on lucky guess(non-deterministic), but if solved deterministically, it takes 2^n time. It takes exponential time, not polynomial time. As the input size increases, it increases exponentially

NP-hard:

Hardest NP problem

When all NP problems can be reduced to a problem A in polynomial time, then that A is NP-hard

NP-complete:

It is an NP-hard problem while also being an NP problem.

Applications

1. Cryptography:

Security of cryptography often ensured by the complexity of a computational task. if P = NP, Almost all passwords become unsafe. it means that even someone who doesn't know the password can find it in polynomial time. Although the question of what degree polynomial it will be remains, if it becomes a P problem, we can reduce the degree through research, so the current encryption system is easily collapsible.

2. Optimization:
Optimization problems can represent real-world problems like scheduling, routing, and resource allocation. If P = NP, then solving these problems efficiently would lead to significant improvements in industries like transportation, logistics, and finance.